Products
What is CoreShell?
A core shell particle consists of a non-porous core in the center and a porous layer outside of the core.
A core-shell structure makes theoretical plate increase 50%, so that a 2.6 μm core shell particle column shows the same theoretical plate as a 1.8 μm totally porous particle column.
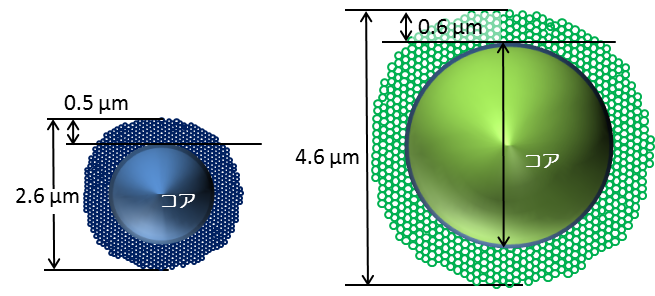
Schematic view of a core-shell silica
Why core-shell particles, the better performance?
Van Deemter
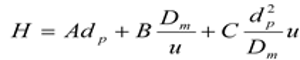
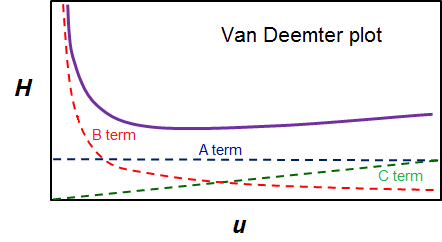
- A term
- Eddy diffusion (dp is particle diameter)
- B term
- Longitudinal diffusion (Dm is diffusion coefficient)
- C term
- Mass transfer
H(height equivalent of one theoretical plate) represents the column length per one theoretical plate. The lower the H, the higher the performance.
Van Deemter plot is a curve using the value derived from the above equation as a function of the theoretical plate height and u (mobile phase linear velocity). Van Deemter Equation contributs A, B and C term individually.
A core-shell particles can be reduced all the values of these three terms.
The size distribution of a core shell (SunShell) particle is much narrower than that of a conventional totally porous particle, so that the space among particles in the column reduces and efficiency increases by reducing Eddy Diffusion (multi-path diffusion) as the A term in Van Deemter Equation.

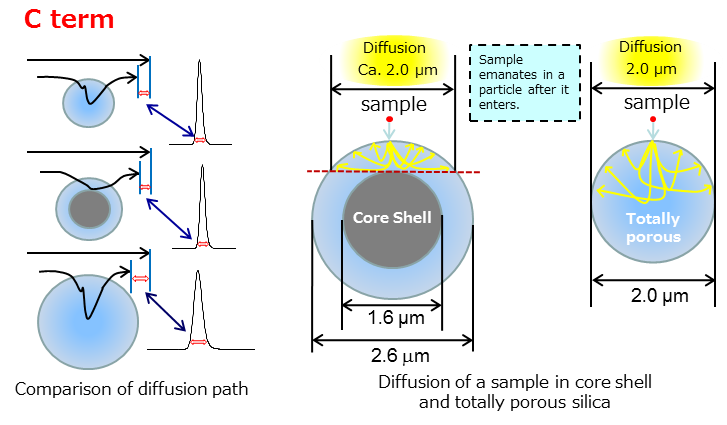
Diffusion of a solute is blocked by the existence of a core, so that a solute diffuses less in a core shell silica column than in a totally porous silica column. Consequently B term in Van Deemter Equation reduces in the core shell silica column.
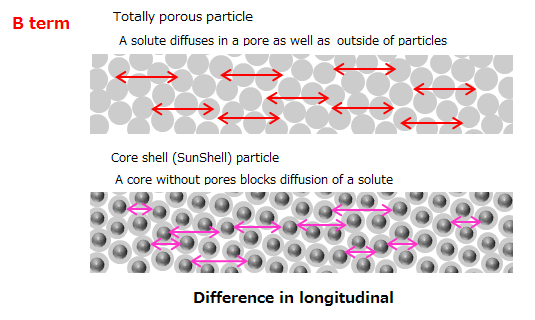
As shown in the below figure, a core shell particle has a core so that the diffusion path of samples shortens and mass transfer becomes fast.
This means that the C term in Van Deemter Equation reduces. In other words, HETP (theoretical plate) is kept even if flow rate increases.
A 2.6 μm core shell particle shows as same column efficiency as a totally porous sub-2 μm particle.
SunShell series is here using the core-shell particles!